Um eine Rüttelanlage korrekt auszulegen und abzustimmen, muss in erster Linie die benötigte Fliehkraft berechnet werden. Sie bewirkt die Beschleunigung, die jeder Partikel der Masse, die bewegt werden soll, erfährt.
Ist die Fliehkraft zu niedrig, wird sich der Partikel nicht bewegen, er verharrt im Ruhezustand. Ist sie zu hoch, führt er neben der zur Verdichtung notwendigen Bewegung z.B. Wanderbewegungen aus, die beim Verdichten (im Gegensatz zum Fördern) unerwünscht sind.
Für die Größe der erzeugten Fliehkraft ist die Masse mu der Unwucht, der Abstand e ihres Schwerpunktes von der Drehachse und die mechanische Schwingfrequenz fm des Motors ausschlaggebend.
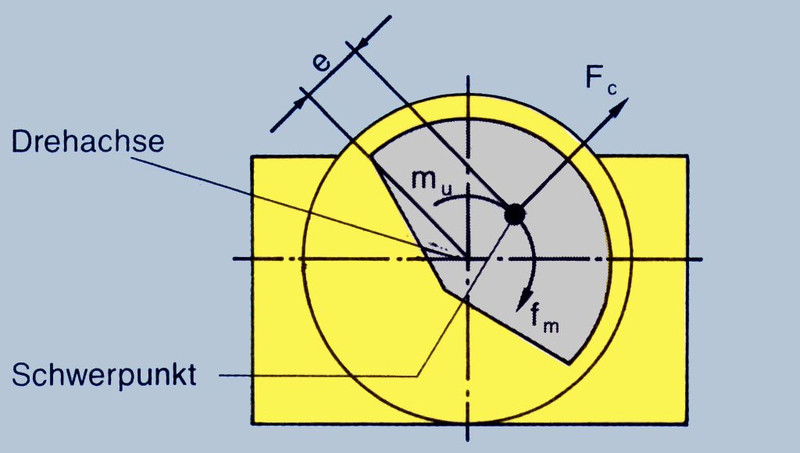
- Abb. 8: Entstehung des Unwuchtmoments Mu = mu ⋅ e
Fc = mu ⋅ e ⋅ ω² / 1000
ω = 2 π ⋅ fm
Fc – Fliehkraft in kN
mu – Masse der Unwucht
e – Abstand des Unwuchtschwerpunktes von der Drehachse in m
fm – mechanische Schwingfrequenz des frei schwingenden Rüttlers 1/s
ω – Winkelgeschwindigkeit der umlaufenden Unwucht in 1/s
In Katalogen ist die minimal und maximal einstellbare Fliehkraft als Nennwert bei Synchrondrehzahl angegeben, da es sich mit diesem Wert leichter rechnen lässt. Die Synchrondrehzahl eines Drehstrom-Asynchronmotors errechnet sich aus der elektrischen Netzfrequenz und Polpaarzahl.
Motordrehzahl
ns = 60 ⋅ fel / p
ns – Synchrondrehzahl in 1/min
p – Polarpaarzahl
fel – elektrische Netzfrequenz
Die Synchrondrehzahl wird bei Belastung um den Schlupf des Asynchronmotors verringert, und so ergibt sich die Betriebsdrehzahl.
N =ns ⋅ (1-σ)
n – Betriebsdrehzahl (mechanische Schwingfrequenz) in 1/min
σ – Schlupf
Bei der etwas kleineren Betriebsdrehzahl ist also Fc um den Faktor (1-σ)2 verringert.
Der Drehstrom-Asynchronmotor hat den Vorteil, dass die erzeugte mechanische Schwingfrequenz bei Belastung gegenüber dem Leerlauf nur geringfügig (um den Schlupf) vermindert wird. In der Praxis ist die Masse der Unwucht mu unbekannt; bekannt sind die Masse m, die in Schwingung versetzt werden soll, und die Beschleunigung a. Für die verschiedenen Anwendungsgebiete liegen für a vielfache Erfahrungswerte vor (siehe Erfahrungswerte). Deshalb bestimmt man Fc (kN) nach der Gleichung:
Berechnung der Fliehkraft in der Praxis
Fc = m ⋅ a / 1000
m – Summe der Massen in kg, die in Schwngung versetzt werden sollen. Das sind:
- Masse der Rüttler mR
- Masse der Rüttelvorrichtung mT
- 10-15% der Masse des zu verdichtenden Stoffes ms
m = mR + mT + ms
a – Beschleunigung in m/s2
Außerdem muss ein Kennwort für die Steifigkeit und das Resonanzverhalten der Vorrichtung berücksichtigt werden.
Die Fliehkraft Fc versetzt die gesamte Vorrichtung zusammen mit der zu verdichtenden Masse in Schwingungen. Die an der Vorrichtung gemessene Schwingungsbreite s darf nicht zu groß sein, da sonst die Rüttelvorrichtung beschädigt werden kann, Wenn die Schwingungsbreite nicht gemessen werden kann, muss man sie errechnen. Die Beschleunigung a ist entweder bereits bekannt oder wird aus Tabelle 4 entnommen.
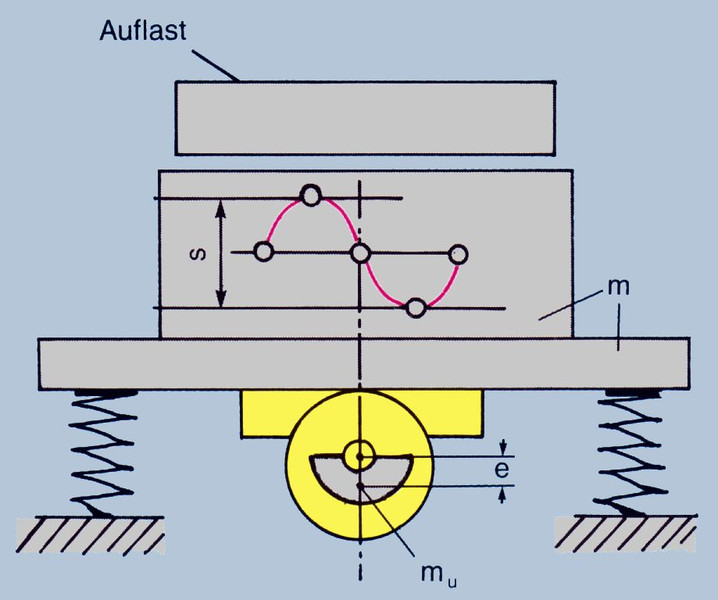
- Abb. 9 Schwingungsbreite an einer Rütteleinrichtung während einer Umdrehung des Außenrüttlers
Berechnung der Schwingungsbreite
s = a / 5,483 ⋅ nT2
s – Schwingungsbreite in mm
a – Beschleunigung in m/s2
nT = n/1000; n: Schwingungszahl in 1/min
Einfluss der Drehzahl auf die Fliehkraft
Da man häufig Frequenzumformer einsetzt, um die Drehzahl der Außenrüttler zu verändern, ist es wichtig zu wissen, welchen Einfluss die Änderung der Drehzahl n auf die Schwingungsbreite s und die Fliehkraft Fc hat.
Aus Formel 1 folgt, dass sich die Fliehkraft bei sonst gleichen Bedingungen quadratisch zur Drehzahl ändert. Das heißt, dass z. B. eine Halbierung der Drehzahl eine Viertelung der Fliehkraft zur Folge hat. Umgekehrt wird die Fliehkraft vervierfacht, wenn die Drehzahl verdoppelt wird. An der Größe der Schwingungsbreite s ändert sich hingegen nichts.
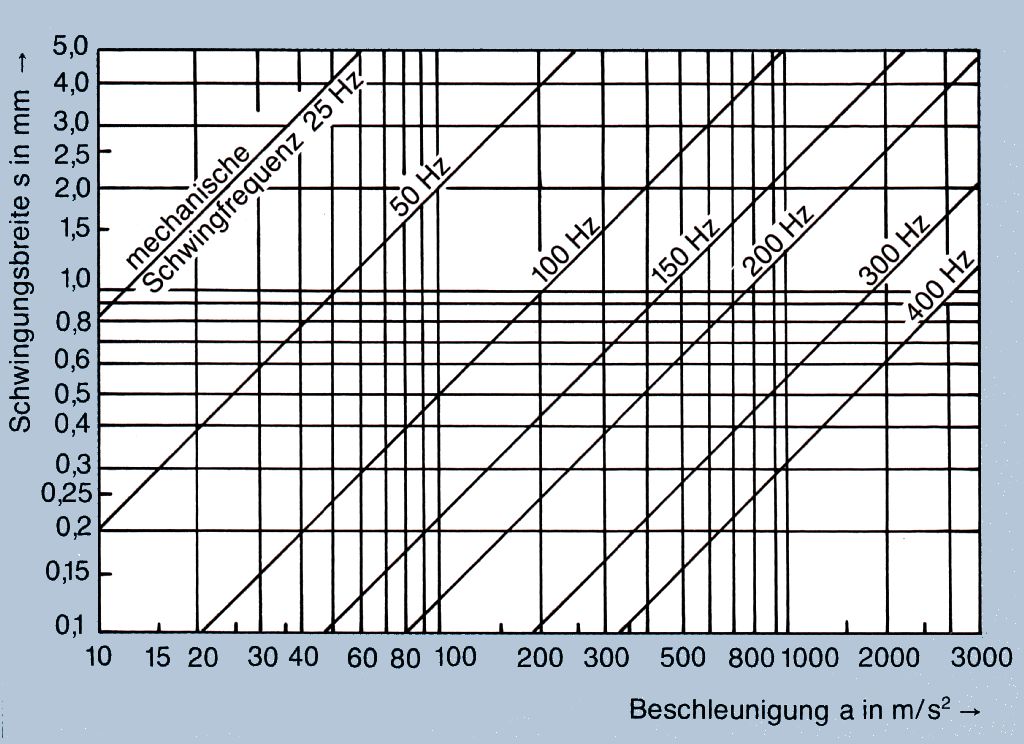
- Abb. 10: Zusammenhang zwischen Schwingungsbreite, Beschleunigung und mechanischer Schwingung
Die Schwingungsbreite s ergibt sich aus der Beziehung
s/2 ⋅ m = mu e
MU = mue
s = (2 ⋅ Mu) / m ⋅ 10
Mu – Unwuchtmoment; 2 ⋅ Mu = Arbeitsmoment MA in kgcm
m – Summe aller bewegten Massen in kg


 DE
DE EN
EN ES
ES
